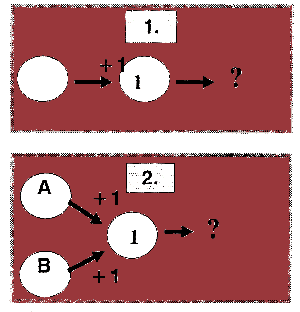
These diagrams are to encourage you to think about the patterns of interactions
which could occur between neurons.
The circles represent neurons. Letters within these are for identification purposes. A number is shown within the circle which indicates the "threshold" for that neuron, i.e. the net input required for it to fire and give an output signal; if no threshold is given, assume a value of 1.
Arrow-heads represent synaptic connection between cells, the strength of which is shown with an indication of whether excitatory (+) or inhibitory (-). The effects of spatial and temporal summation are relevant.
These interactions are most easily appreciated in terms of single, discrete action potentials, but should also be considered in terms of rates of firing, i.e. bursts of spikes, as well as graded inputs and spontaneous firing by the cell(s).
You can check out the descriptive terms for the different integrative patterns.
Boxes 1 and 2 give you a nice easy start, involving straightforward,
excitatory inputs and a threshold of 1 in the cell.
Contrast the situation in box 2 with that in box 3, where the threshold
is increased to 2,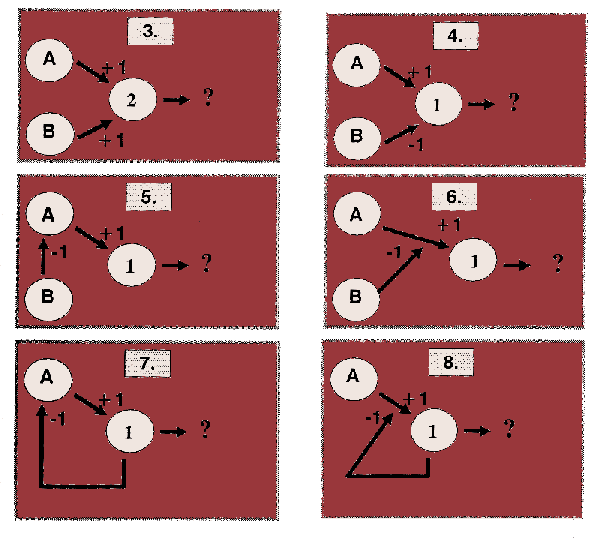 
and
box 4 where we now have one excitatory and one inhibitory input.
Things start to get a little more interesting as you work through boxes
5 to 8.
Check out the descriptive terms
Now figure out what happens as you go through the loops in boxes 9 to
11.
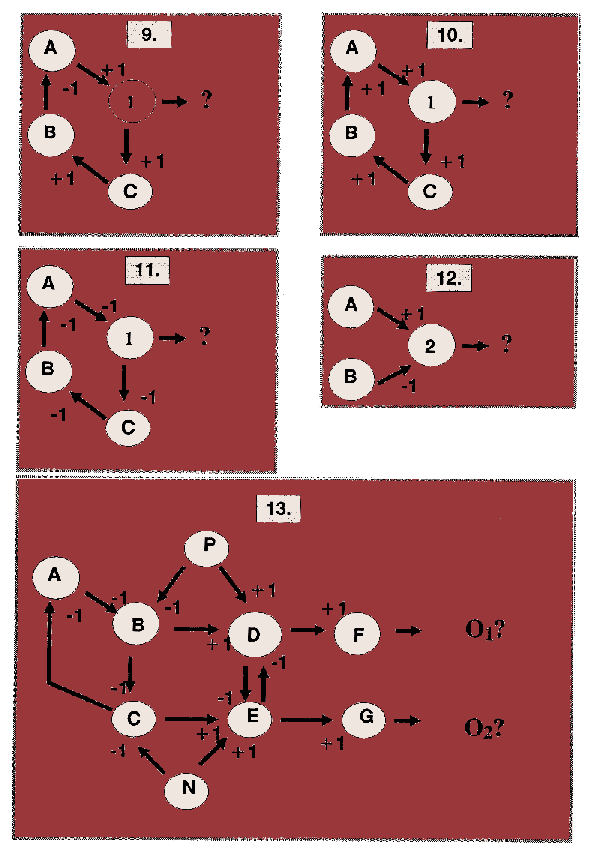
In box 12 we're back to a simple 2-on-1 situation,
but now with a not-so-simple input of one excitatory and one inhibitory,
with a threshold of 2! - what's needed now for us to get an output?
Box 13 is much more interesting - can you work out how it works?
Note that we have two outputs from the circuit in box 13.
Check out the descriptive terms
In the next two boxes, we are again interested in a pair of outputs.
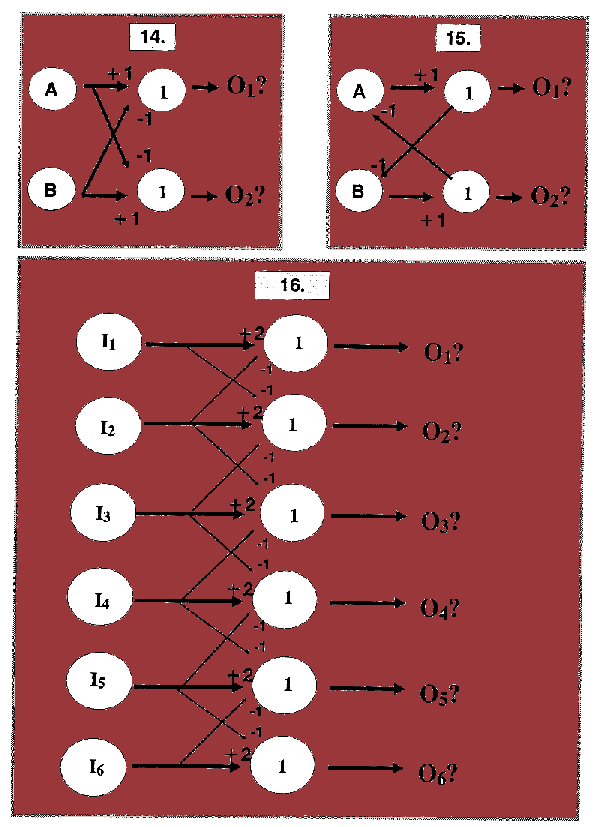
In boxes 14 and 15, what is the inter-relationship between the two outputs (O1 and O2)?
How does the flow of information along one channel (from A) affect the informaion along the other (from B)?
The final example extends from just two outputs to an array (O1
to O6), but based on the same principles as in box 14.
What happens with different patterns of inputs, like these two examples?
|
|
|
|
|
| 0 |
|
0 |
|
| 1 |
|
0 |
|
| 2 |
|
0 |
|
| 4 |
|
10 |
|
| 8 |
|
10 |
|
| 16 |
|
10 |
|
Try with other values of inputs and also for larger arrays, as well as with different values for the lateral inhibition and thresholds.