Ecological Sampling Methods

Back to HATs

A. Census

Count entire population.
Really possible only with very obvious individuals and ability to cover entire spread of population range (e.g. census of human population in Britain).

B. Sample

Count just part of the population and then extrapolate to estimate total population size.
Need to know how reliable samples are and the degree of errors involved when extrapolating depends a lot on variability across the range of the population).

1. Direct counts

a) Relevé - for vegetation sampling (Mueller-Dombois & Ellenberg)

b)Quadrats - depending on size and shape, as well as number and distribution; size will depend on sizes of plants being recorded and diversity of habitat.
Shapes: square, rectangular, circular, hexagonal. Linear samples (transects) and point quadrats also possible.
Could also be used for animals (especially sedentary species).

c) Capture techniques for animals:

  1. Pitfall traps (for invertebrates active on/near soil surface)
  2. yellow (water) trays (for flying insects)
  3. sticky traps (e.g. for aerial plankton, or on tree trunks)
  4. suction traps (for aerial plankton, or for fish)
  5. corrugated paper traps (wrapped round tree trunks)
  6. nets (e.g. fishing, sweep-nets for invertebrates in vegetation)
  7. beating trays
  8. "knock-down" gasses and collectors
  9. photo-eclectors
  10. hand capture (relates to unit-effort sampling designs).

2. Indirect counts

a) Evidence of animals' presence:
  1. leaf scars by leaf-mining insects
  2. nests (e.g. ants, birds)
  3. dung, droppings, owl pellets, etc.
  4. damage to vegetation (e.g. bark stripped from trees)


b) Evidence from human activities:

  1. fishing quotas and catch rates
  2. pelt returns by hunters (e.g. Hudson Bay Company records over long time).


Many of these methods are dependent on parameters in addition to the simple abundance of the species being sampled. Thus, pitfall traps are dependent on the level of activity of the animals as well as their density. The indirect methods are also dependent on the intensity of the human activities (e.g. how many hunters) and the accuracy of the records.

The particular type of statistical analysis to be applied to the data (whether just descriptive or inferential to sort out relationships and effects) will depend on how the data behave (patterns of errors, variability, etc.) which in turn will be effected by the particular sampling method(s) used to obtain the data.

C. Sampling Designs

two-habitat environment
 
 

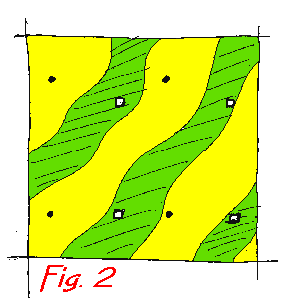
Imagine that you are sampling for spiders in an environment which comprises two contrasting habitat types as in this diagram (Figure 1).

The shaded/green and clear/yellow areas have different types of vegetation and you want to use pitfall traps to sample the ground-active spiders.

You also want to use quadrats to sample the plants growing there and use these data to quantify the differences in habitat conditions corresponding to the positions of your pitfall traps (or clusters of traps).

Where should you place your pitfall traps (or clusters) and your plant-survey quadrats?
 
 
 

1. Regular / Uniform

regular sampling
 
 

Grid:

Samples are arranged in a regular pattern such as lines, rectangular arrays, hexagonal patterns.
This arrangement of samples could possibly miss heterogeneous patches in sample area; the black dots miss the shaded/green areas and the open squares don't sample the clear/yellow areas in Fig 2.).
Depending on sample size and distribution of samples, this sampling pattern may be inadequate.
 
 

Transects:

This is when samples are arranged in lines, not necessarily straight, to cover range of variation in sampled area (viz. lower line of four samples in Fig. 2).
 
 

2. Random

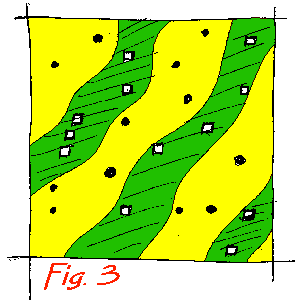
Samples are located randomly (preferably using random number generator or tables relative to grid coordinates).stratified random sampling

If sample size is too small might miss out heterogeneous patches altogether (viz. black circles or open squares in Fig. 3); even with larger sample size might sample different patches disproportionately to their relative areas.
 
 
 

3. Stratified random

Samples are located randomly (as in 2. above), BUT allocating samples deliberately to each of the recognised different environmental patches in the sample area. The number of samples in a patch type should be proportional to the area (and possibly the diversity) of the patch type.
The combined samples in the black dots and the open circles in Fig. 3. portray a stratified random sampling approach.
 

This is my preferred strategy.

 

 
 

Back to HATs